这节课主要讲的是无线的加密,首先了解一下无线的特性。
无线是向四面八方传播的无线电波,因此谁都能检测到,截获到,并且这个流程非常简单就可以实现。无线网络容易拥堵,因为信道的数量是有限的,特别是2.4G的信道就十几个(11或者13)。因此无线的加密非常重要,比如VPN之类。
这里讲到一个点,无线的传播距离,理论上也就是百米左右,但是实际上穿墙什么的会信号衰减,而在空旷的地方上会远一些。曾经有人在湖边上做实验,发现无线信号可以通过水来扩展,长达7公里。
无线网络有不同的版本

最早的无线加密版本是用WEP,预先共享Key,一共64个bits,包括40 bits的加密和24bits的初始向量,使用RC4加密方式,对称加密和Stream cipher,这样利于传输音视频码流。
从key的bits来看非常不安全,因为只有5个ASCII或者10个十六进制,太短了。然后最多可以设置4个密钥,但是也太少了。
IV即初始向量可以是随机的也可以是顺序的,大部分初始向量都默认为0,之前我们讲了24 bits的初始向量,因此只有2的24次方,真心是数量不多,很容易就用完 然后又重复使用。随机IV大约4000个包后就会出现重复冲突,而顺序IV只要reset到0就开始重复冲突。但是要注意的是一个很差的安全加密方式是远远好于没有安全加密的。
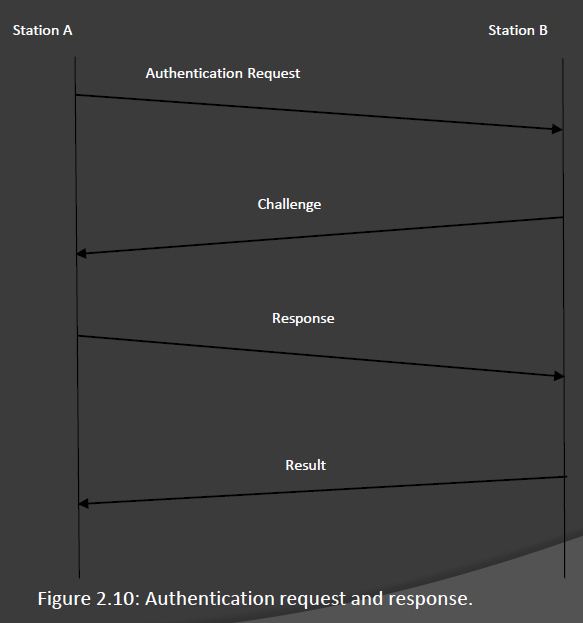
WEP的授权方式如下:
RC4的加密似乎不是很复杂,理论上有空可以研究一下,用来暴力破解。
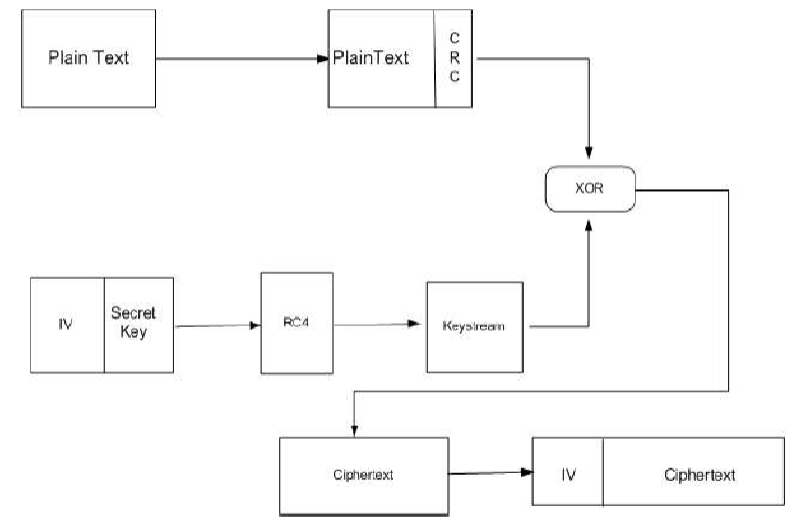
下面这个公式讲了两个明文使用了一样的iv和key的结果,而实际上这就是wep的缺点
If C1 = P1 XOR RC4(iv,k)
And C2 = P2 XOR RC4(iv,k)
Then
C1 XOR C2 = (P1 XOR RC4(iv,k)) (P2 XOR RC4(iv,k))
= P1 XOR P2
In other words, XORing the two ciphertexts that have been encrypted with the same IV and key together causes the keystream to cancel out and the result is the XOR of the two plaintexts. This can lead to a number of different attacks. Firstly, if the plaintext of one of the messages is already known (known plaintext attack) the plaintext of the other can be easily discovered. Secondly, even if neither plaintext is known, an attacker can simply try different combinations until likely words are discovered.
我们已知WEP是不安全的,所以后面2003年WIFI联盟又推出了新的加密WPA,Wi-Fi Protected Access。这是一个紧急推出的临时方案,也是使用预先分享的key。使用了TKIP – Temporal Key Integrity
Protocol。IV改成了48个bits,所以就有2的48次方,这样重复的概率就大大降低了281 474 980 000 000 (281 trillion)。
之后呢2004年WIFI联盟推出了正式方案即WPA2,使用AES加密(Rijndael加密法,就是一轮一轮又一轮那个加密),最重要的是开始使用AAA协议或者RADIUS服务
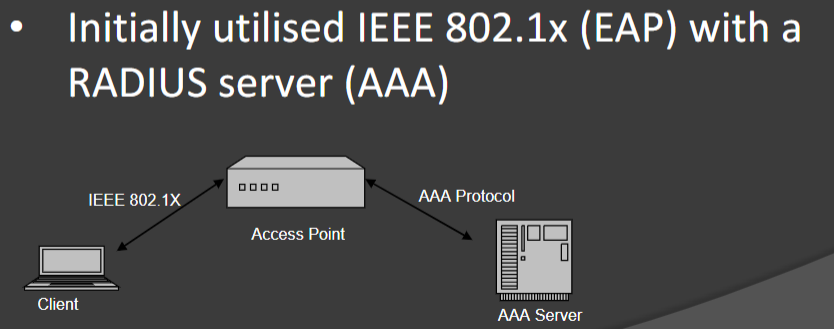
2018年WIFI联盟又推出了新的WPA3标准,包括了个人版和企业版。使用 Simultaneous Authentication of Equals (SAE),企业版同样和WPA2一样使用 IEEE 802.1x (EAP) with a RADIUS server (AAA)。最少的加密长度为Optional 192 bit minimum encryption
此外还有以下特点,第三点是椭圆曲线的DH算法。
• 256 bit Galois / Counter Mode
• 384 bit Hashed Message Authentication (HMAC)
• Elliptic Curve Diffie Hellman
• Wi-Fi Protected Open - optional
简单的对比一下
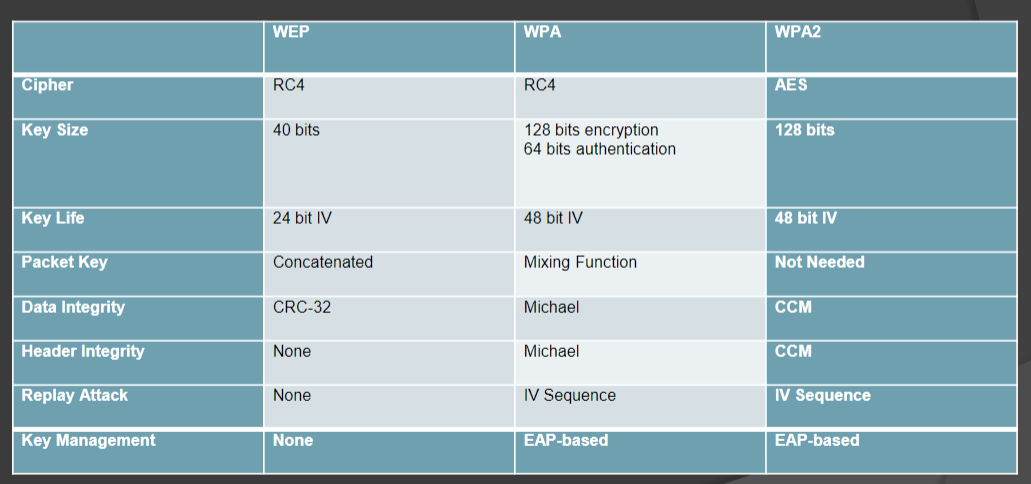
此外key的交换方式也有直接或者KDC的方式两种。
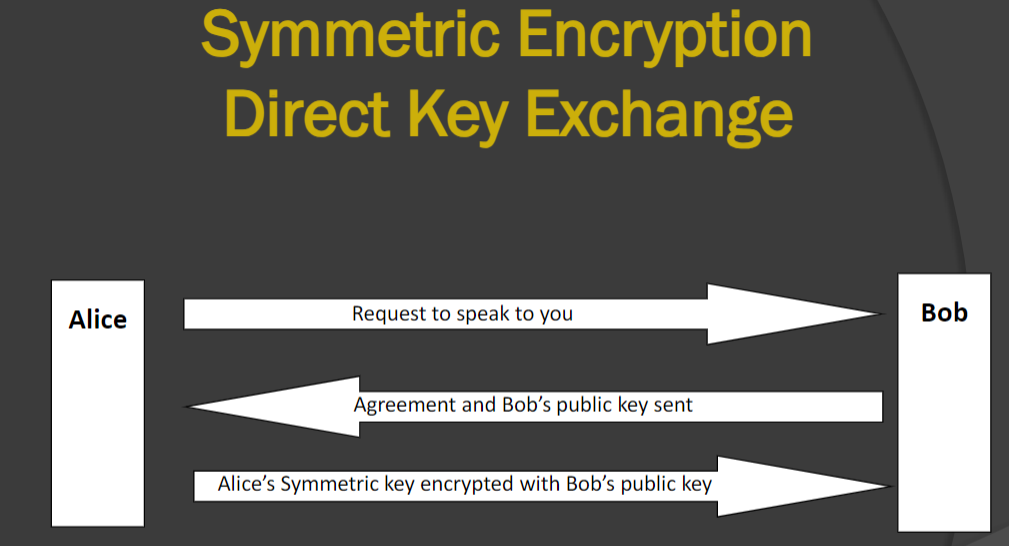
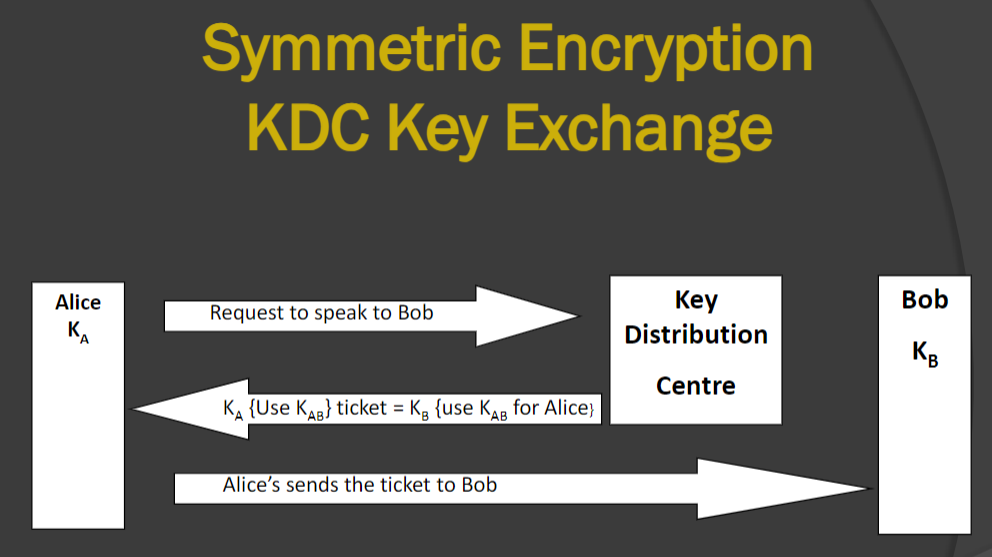
好啦,那么针对无限的攻击方式有很多
• Man in the Middle (MitM) 中间人攻击,之前讲过,在AP和client之间分别与双方建立连接然后截获信息。
• Packet Injection – packets accepted replayed
• ARP Poison
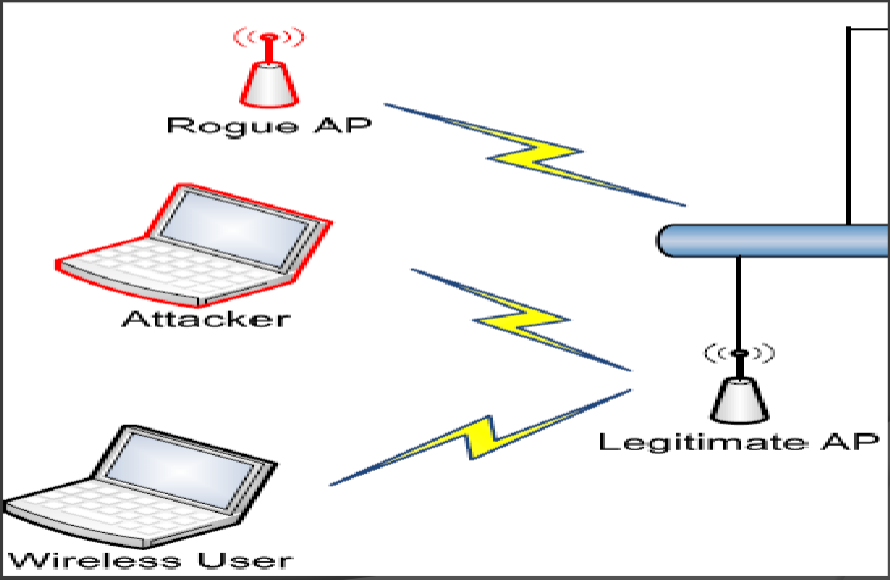
• Fake AP
• Wardriving – Crimes Amendment Act 2003这个目前还不能讲是否违法
• Netstumbler & InSSIDer 这两个软件是用来wardriving的,可以回头研究一下。
然后讲了一些法律,关于这个行为是否违法。。。。其中很多法条都很难界定,比如是不是主观意义还是客观无意的,是否得到授权等等。下图表示了一个违法案例。
一些其他安全隐患,比如WDS,无线桥接/中继系统,这里讲了一些细节,具体我也没听太明白,总之就是不同的AP之间切换有隐患
• Wireless Distribution System
• Channel sharing
比如WPS,一般是AP上有个按钮之类的可以快速联网,但是这个只有8个digits,而且是分为2个部分,也是隐患
• WiFi Protected Setup
• Designed to be simple to implement security
• 8 digit (10 million possible combinations of numbers)pin stored as 2 x 4 digits(10 thousand + 1 thousand possible combinations of numbers)
为了解决隐患,阻止包被抓取,被未授权的使用,被解读信息
• Prevent packets being captured?
• Prevent unauthorised use?
• Prevent messages being read?
于是又有了FHSS技术,也就是跳频技术。Frequency-Hopping Spread Spectrum
后面讲了一大堆都是关于AD HOC/ IoT 网络的以及安全问题,几十页的ppt,我当时没听懂,PPT也看不懂,这个需要抽空研究一下。
Wireless ad hoc network无线随意网络,mobile ad hoc network, 缩写为WANET, MANET
那么实验课部分,没啥特别的,除了之前讲的cryptool工具以外,这节课引入了Kali,利用两个科学计算器来计算一些加密结果。
首先来计算RSA加密算法,
RSA也是基于DH算法加密,不过略有区别,
m = message in decimal numbers.
c = ciphertext
e = public key exponent
d = private key
RSA Encryption:
C = (me) mod n
RSA Decryption:
M = (Cd) mod n
首先是随机找两个素数p和q,这里我们假设p用11,而q用13
接下来计算模数modulus (n),n=p * q = 143,注意这里n的值很小是因为这是演示用的,实际上RSA算法用非常大的素数,因此n的值也超级大,所以很难逆向破解找出p和q的值。
然后需要计算欧拉函数Totient: φ(n)=(p−1) (q−1)=(11-1)*(13-1)=120,同上,这个数字很小也是因为演示用
下一步可以一开始就实行,选一个public key (e),和p q一样必须是随机的素数,而且必须小于n,也不能和p q任一个相等。一般来说e会选择的小一点,因为可以减少计算时间,增加计算效率。我们这里选择e = 7
The public key (e) should be:
a) A random prime number
b) A co-prime to φ(n) (Share a gcd of 1 with φ(n) and be less than φ(n) All prime numbers
less than φ(n) and not a factor of φ(n) will be coprime to φ(n))
这样我们就得到了公钥 Public Key = (7, 143)
接下来需要计算私钥,Private Key exponent (d)
The private key is determined by finding the 乘法倒数multiplicative inverse of e (in our case 7) with
φ(n) (in our case 120).
说白了就是通过e和那个欧拉函数来计算,
d = 1 mod 120
当然最简单就是下面的方法,把欧拉函数从1开始乘,然后加1 然后除以e,本例子是7,直到没有余数为止。最后得到的商就是d=103
(120 x 1) + 1 = 121 / 7 = 17 and 2 remainder
(120 x 2) + 1 = 241 / 7 = 34 and 3 remainder
(120 x 3) + 1 = 361 / 7 = 51 and 4 remainder
(120 x 4) + 1 = 481 / 7 = 68 and 5 remainder
(120 x 5) + 1 = 601 / 7 = 85 and 6 remainder
(120 x 6) + 1 = 721 / 7 = 103 and zero remainder
这样我们就得到了私钥Private Key = (103, 143)
通过cryptool会计算的更加快。
Cryptool内置了大量工具,比如通过n来计算p和q,通过两个使用了相同p的公钥找出两个p和两个q。
Example with the xxd command converting characters to hex is:
>echo “This is a s3cret passw@rd?” | xxd -ps
而Kali Linux里则内置了openssl和genius两个科学计算器,也可以用来辅助计算。
一些常见命令,
openssl>prime 999 可以判断999是不是素数
Openssl>prime -generate -bits 6 生成一个6 bits的素数
而在Genius里,
PrimeFactors(150)可以分解150
gcd(58,52)可以找到连个数字的公约数
MaxDigits=256 可以让最大digits到256 位,不然默认的话大的数字会显示有问题
IntegerOutputBase=16 可以改变显示的格式,16禁止等等
IsPrime(999)可以判断是不是素数
之前加密加密可以直接计算
C = M^e mod (65) => 33^5 mod (65) = (39135393 mod 65) = 602082 and 63 remainder

